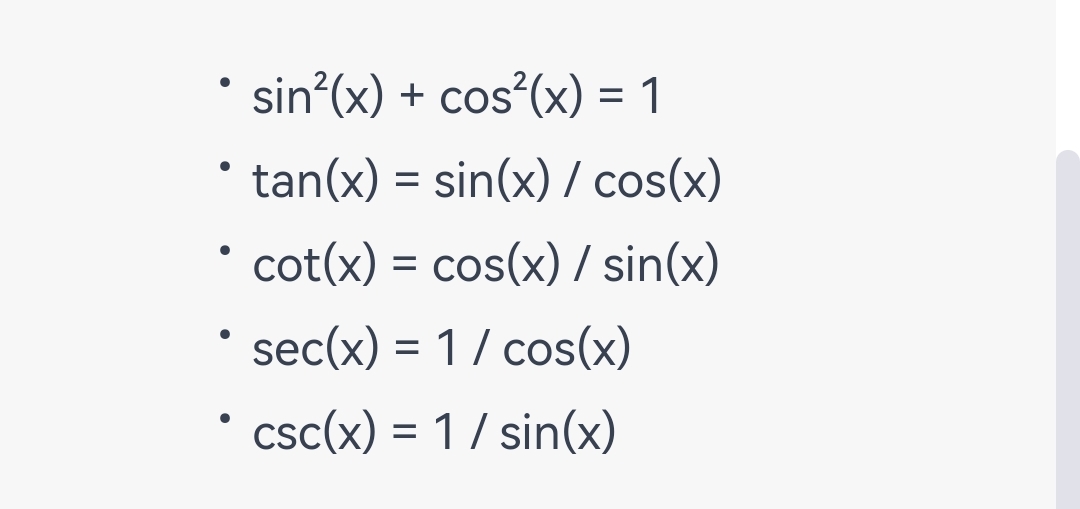Physical science grade 11 exam papers and memos 2022 pdf download

Physical science grade 11 exam papers and memos 2023 pdf download

Grade 11 Past Exam Papers and Memos

• Grade 11 Physical Sciences March Exam Paper.pdf

• Grade 11 2022 June Exam Paper 1 Download

To pass a Grade 11 Physical Sciences exam, here are some tips and strategies you can follow:

1. Attend classes regularly and pay attention: Physical Sciences is a complex subject, and attending classes regularly and paying attention to what is taught can help you understand the concepts better.

2. Create a study schedule: Allocate time for studying and revising Physical Sciences. Make sure to include time for practicing past papers and completing assignments.

3. Understand the concepts: Physical Sciences involves a lot of theory and mathematical calculations. Make sure you understand the concepts and formulas thoroughly.

4. Practice regularly: Practice solving problems regularly, and attempt past papers to get familiar with the exam format and types of questions that may be asked.

5. Seek help when needed: Don't hesitate to ask your teacher for help if you are struggling with a concept. You can also form study groups with your classmates and work on problems together.

6. Revise regularly: Revise the material regularly, especially the important concepts and formulas.

7. Stay calm and confident: Nervousness and anxiety can negatively impact your performance during an exam. Stay calm, take deep breaths, and be confident in your abilities.

8. Don't cram: Cramming the night before the exam is not an effective way to learn or retain information. Instead, try to study in advance and get enough rest the night before the exam.

9. Use visual aids: Physical Sciences involves a lot of diagrams, graphs, and other visual aids. Make sure you understand how to read and interpret these visual aids, and use them to your advantage during the exam.

10. Stay up to date: Physical Sciences is an evolving subject, and it's important to stay up to date with the latest developments and trends. Subscribe to science magazines or newsletters, and follow relevant social media accounts or blogs to stay informed.

11. Stay focused during the exam: Read the instructions and questions carefully, and allocate your time wisely. If you get stuck on a question, move on to the next one and come back to it later.

Remember that passing an exam is not the end goal. The goal is to understand the concepts and develop a passion for Physical Sciences. By following these tips, you can not only pass your Grade 11 Physical Sciences exam but also develop a deeper appreciation and understanding of the subject.

Mastering Trigonometry: Unveiling the Secrets of Sine, Cosine, and Tangent for Optimal Problem Solving and Mathematical Success

Trigonometry deals with the relationships between angles and the sides of triangles. The most basic trigonometric functions are sine, cosine, and tangent. These functions have a wide range of applications in mathematics, science, engineering, and many other fields.

There are many techniques for solving trigonometric equations and identities, but there is no general formula that can solve every trigonometric equation. However, there are some general strategies that can be applied to a wide range of problems.

One of the most important strategies is to use the fundamental trigonometric identities, which relate the trigonometric functions to each other. For example:

Another strategy is to use the unit circle, which is a circle with a radius of 1 centered at the origin of a coordinate system. By placing an angle in standard position (with its initial side along the positive x-axis), we can determine the sine, cosine, and tangent of the angle by considering the coordinates of the point where the terminal side of the angle intersects the unit circle.

Trig identities are equations involving trigonometric functions that are true for all values of the variables.

Other strategies include using the addition and subtraction formulas, the double-angle formulas, and the half-angle formulas, which can be used to simplify trigonometric expressions and solve trigonometric equations.

The general solution for trigonometric equations contains an infinite number of solutions that can be expressed as:

Overall, while there is no single general formula for solving every trigonometric equation, there are a variety of techniques and strategies that can be applied to a wide range of problems.

Mastering Trig Equations: Unleashing the Power of the General Solution!

The general solution for trigonometric equations contains an infinite number of solutions that can be expressed as:

x = θ + 2πn, where n is an integer.

This applies to both sine and cosine functions.

For example:

Find the general solution to the equation cos(x) = -1/2.

Step 1: Find the reference angle

cos(x) = -1/2 has solutions in the second and third quadrants, where the reference angle θ is 60 degrees.

Step 2: Write the general solution

cos(x) = -1/2 has two solutions in each quadrant. Therefore, the general solution to this equation is:

x = 120 degrees + 360n or x = 240 degrees + 360n.

Where n is an integer, which can take values such as -2, -1, 0, 1, 2, ... etc.

Trig identities are equations involving trigonometric functions that are true for all values of the variables.

By substituting these values of n into the general solution, we can find all of the possible solutions for the given trigonometric equation.

Apartheid essay 300 words grade 11

Apartheid was a system of institutionalized racial segregation that existed in South Africa from 1948 until the early 1990s. It was a policy that enforced discrimination against non-white citizens in various aspects of life, such as education, employment, housing, and political representation.

The origins of apartheid can be traced back to the colonial era, where white Europeans began to settle in South Africa and dominate the land and resources. In 1948, the National Party, which was predominantly made up of white Afrikaners, came to power and began to enforce apartheid laws.

The apartheid regime divided the population into four racial groups: white, black, colored, and Indian. The laws ensured that the white minority had access to the best opportunities and resources, while the non-white majority was relegated to inferior conditions. Non-white citizens were forced to carry identity documents, which restricted their movements and made it difficult for them to travel or find work.

The apartheid system was met with resistance from various sectors of society. Activists such as Nelson Mandela and Desmond Tutu were instrumental in the fight against apartheid. The African National Congress (ANC), led by Mandela, organized protests, boycotts, and acts of civil disobedience. The international community also played a role in isolating South Africa through economic sanctions and diplomatic pressure.

Finally, in 1990, President F.W. de Klerk announced that the apartheid laws would be abolished, and Mandela was released from prison after 27 years. In 1994, South Africa held its first democratic elections, and Mandela became the country's first black president.

In conclusion, apartheid was a dark period in South Africa's history that institutionalized racial segregation and discrimination. The legacy of apartheid is still felt today, as the country continues to struggle with issues of inequality and social justice. However, the end of apartheid is also a testament to the power of activism, resistance, and solidarity in the face of injustice.

Mastering Quadratic Equations: Simple Steps for Solving Math's Toughest Challenges!

A quadratic equation is an equation of the form ax² + bx + c = 0, where a, b, and c are constants and x is the variable. Here is an example of how to solve a quadratic equation:

Let's solve the quadratic equation x² + 2x - 3 = 0

Step 1: Identify the values of a, b, and c

Here, a = 1, b = 2, and c = -3

Step 2: Find the discriminant (b² - 4ac)

The discriminant is b² - 4ac = 2² - 4(1)(-3) = 16

Step 3: Use the discriminant to determine the nature of the roots

If the discriminant is positive, then there are two real roots.

If the discriminant is zero, then there is one real root.

If the discriminant is negative, then there are no real roots.

In this case, since the discriminant is positive, we know that there are two real roots.

Step 4: Solve for x using the quadratic formula, which is:

x = (-b ± √(b² - 4ac)) / 2a

Substituting the values of a, b, and c, we get:

x = (-2 ± √(2² - 4(1)(-3))) / 2(1)

x = (-2 ± √16) / 2

x = (-2 ± 4) / 2

This gives us two possible solutions:

x = (-2+4)/2 = 1

x = (-2-4)/2 = -3

So the roots of the quadratic equation x² + 2x - 3 = 0 are x = 1 and x = -3.

explain how making early arrangements for higher education could minimise the stress of having to rush after receipt of results

Making early arrangements for higher education can help minimize the stress of having to rush after receipt of results in several ways:

1. More time for planning: By starting the planning process early, you have more time to research and explore different options, such as different institutions, fields of study, and financial aid opportunities. This can help you make more informed decisions, which can reduce stress and anxiety when the results are released.

2. Better preparation: If you start preparing for higher education early, you may have more time to develop the necessary skills and knowledge needed to succeed in your chosen field of study. This can help build confidence and reduce stress when the results are released.

3. Higher chances of acceptance: Many universities and colleges have limited space, and competition for available spots can be fierce. By starting the application process early, you increase your chances of gaining acceptance, which can reduce the stress of having to rush to find alternatives. 

In summary, making early arrangements for higher education gives you a head start and allows you to plan better, which can help reduce stress and anxiety when the results are released.

Recommend what grade 12s could do to minimise the impact of the anxiety they may feel on the day of the examination

Here are some tips for Grade 12 students to minimize anxiety on the day of their examination:

1. Get enough sleep: A good night's sleep can help reduce anxiety and improve concentration on the exam day.

2. Eat a healthy breakfast: A nutritious breakfast helps fuel the brain and can help students feel energized and focused during the exam.

3. Practice relaxation techniques: Deep breathing or meditation can help calm the mind and reduce anxiety.

4. Arrive early: Arriving early for the exam allows time for students to get settled in and mentally prepare before the exam begins.

5. Don't cram: Studying the night before can cause more confusion and anxiety. Students are advised to do a thorough revision in advance and take sufficient rest on the night before the exam.

6. Stay positive: Positive thinking and self-talk can help reduce anxiety and increase confidence.

7. Read instructions carefully: Reading all instructions carefully can help prevent unnecessary mistakes and reduce anxiety.

Making early arrangements for higher education can help minimize stress in several ways

8. Avoid discussing the exam with others: Discussing the exam with peers just before the exam can create unnecessary stress and anxiety.

how making early arrangements for higher education could minimise the stress

Making early arrangements for higher education can help minimize stress in several ways:

1. More time for planning: By starting the planning process early, you have more time to research and explore different options, such as different institutions, fields of study, and financial aid opportunities. This can help you make more informed decisions, which can reduce stress and anxiety.

2. Better preparation: If you start preparing for higher education early, you may have more time to develop the necessary skills and qualities that will help you succeed in your chosen field of study. For example, you might be able to take extra courses or participate in internships or other work experiences that will prepare you for college or university.

Here are some tips for Grade 12 students to minimize anxiety on the day of their examination

3. Fewer surprises: The earlier you start planning for higher education, the more time you have to adjust to any surprises or challenges that may arise along the way. For example, if you need to take a standardized test like the SAT or ACT, you'll be better prepared if you start studying well ahead of time.

4. Reduced financial stress: Early planning also gives you more time to explore financial aid options, such as scholarships, grants, and student loans. By knowing what financial support is available to you, you can feel more confident about your ability to pay for your education.

Exploring Study Options: Choosing the Right Path for Your Academic Journey!

Study options refer to the various paths that students can take to pursue their education and achieve their academic and career goals. Some common study options include:

1. Full-time study: This involves enrolling in a program at a college or university and attending classes on a full-time basis.

2. Part-time study: This involves enrolling in a program at a college or university and attending classes on a part-time basis, which may allow students to work or attend to other responsibilities.

3. Online learning: This involves enrolling in a program that is delivered entirely online, which may offer greater flexibility and convenience for students who cannot attend classes in person.

4. Distance learning: This involves enrolling in a program that is delivered through a combination of online learning and correspondence, which may be suitable for students who live far from a college or university.

5. Apprenticeships: This involves working in a skilled trade or profession and receiving training on-the-job, which may lead to certification or licensing in a particular field. 

6. Vocational education and training: This involves enrolling in a program that provides hands-on training in a specific trade or profession, which may lead to certification or licensing in that field.

7. Study abroad: This involves enrolling in a program at a college or university in a different country, which may offer students the opportunity to experience different cultures and gain international experience.

8. Graduate studies: This involves pursuing advanced studies beyond the undergraduate level, such as a master's or doctoral degree, which may prepare students for leadership roles in academia, research, or industry.

9. Professional development: This involves taking courses or attending workshops to develop new skills or enhance existing ones, which may be suitable for professionals who want to improve their job performance or advance their careers.

10. Open education: This involves accessing educational resources and courses that are freely available online, which may allow students to learn at their own pace and according to their own interests.

11. Continuing education: This involves enrolling in courses or programs to acquire new skills or knowledge in a particular area, which may be suitable for professionals who want to update their skills or change careers.

Two factors to be considered when choosing a career

Overall, there are a wide variety of study options available to students, each with its own benefits and challenges. Choosing the right study option will depend on a student's individual needs, goals, and circumstances, as well as their personal preferences and learning style.

Public participation - Decision making

Public participation in decision making is the process by which members of the public are invited to contribute their ideas, opinions, and perspectives to inform and shape decisions that affect their communities. This process can take many forms, including public meetings, hearings, surveys, focus groups, and online forums.

The goal of public participation is to ensure that decisions are made in a transparent and inclusive manner, and that all stakeholders have an opportunity to be heard and to provide input. Public participation can help to increase the quality of decisions by incorporating diverse perspectives and expertise, and it can also help to build trust and support for decisions by ensuring that they are perceived as fair and legitimate.

Effective public participation requires clear communication, a commitment to listen to and consider public input, and a willingness to engage in meaningful dialogue and collaboration with stakeholders. It is also important to ensure that the public has access to the information and resources they need to participate effectively, and that the decision-making process is designed to be inclusive and equitable.