Trigonometry deals with the relationships between angles and the sides of triangles. The most basic trigonometric functions are sine, cosine, and tangent. These functions have a wide range of applications in mathematics, science, engineering, and many other fields.
There are many techniques for solving trigonometric equations and identities, but there is no general formula that can solve every trigonometric equation. However, there are some general strategies that can be applied to a wide range of problems.
One of the most important strategies is to use the fundamental trigonometric identities, which relate the trigonometric functions to each other. For example:
Another strategy is to use the unit circle, which is a circle with a radius of 1 centered at the origin of a coordinate system. By placing an angle in standard position (with its initial side along the positive x-axis), we can determine the sine, cosine, and tangent of the angle by considering the coordinates of the point where the terminal side of the angle intersects the unit circle.
Other strategies include using the addition and subtraction formulas, the double-angle formulas, and the half-angle formulas, which can be used to simplify trigonometric expressions and solve trigonometric equations.
Overall, while there is no single general formula for solving every trigonometric equation, there are a variety of techniques and strategies that can be applied to a wide range of problems.


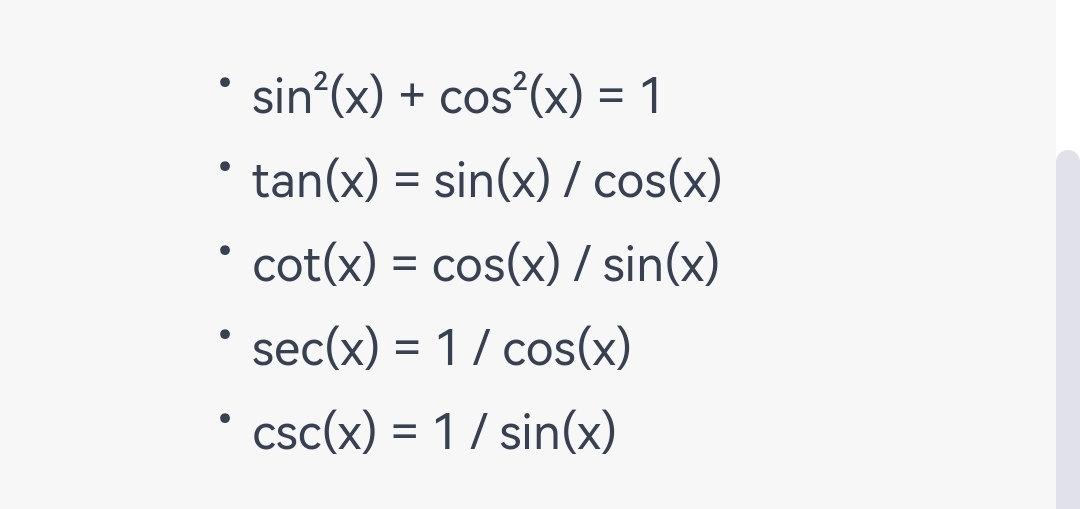




No comments
Post a Comment